MD5加密和Hash函数分析

「 密码学 」 January 03, 2020

MD5加密和Hash函数分析

Words count 111k Reading time 1:41 Read count 0

一、MD5加密算法的原理分析

​ md5的输入是512位的倍数，输出是128位，首先填充消息，使其长度为与448 mod 512同余，即长度是512的倍数减去64，填充的消息第一位是1，后面全部都是0，即使原来的消息长度刚好与448 mod 512同余(64)，仍然需要填充，即使原来的消息长度刚好是512的整数倍，仍需要填充。

​ 再将这剩余的64位填充为原来消息的长度(二进制)，如果原来的消息长度大于64位，则只填充低64位，之后的序列长度就是512的倍数了，这里每一个512位称为一个分组，又将每一个512分为16个32位，称为一个子分组(M0-M15)，之后进行4轮运算，每一轮进行16次操作，分别针对这16个子分组。

原消息有几个分组就进行几次循环，循环这4轮运算，每一次循环需要一个128位序列当“种子”（A=0x67452301；B=0xefcdab89；C=0x98badcfe；D=0x10325476，很明显是小端序存储），之后输出一个128位的序列，这个序列与下一分组继续作用产生下一次的128位的输出。

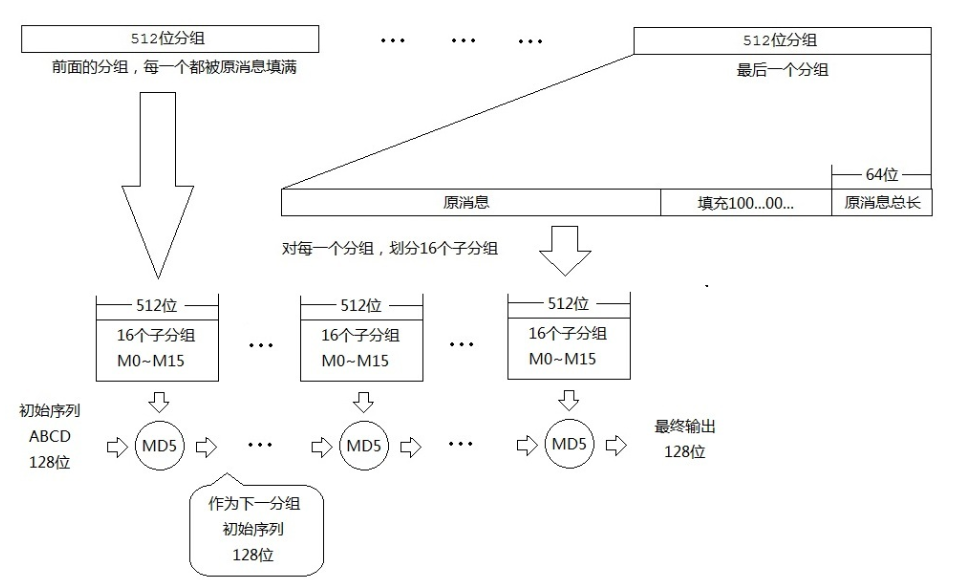
57640062894

下面说说具体的每次循环的4轮运算是怎么样的：

这4轮运算需要用到一个常数表T[i] (i = 1-64),等于4294967296*abs(sin(i))所得结果的整数部分，其中i用弧度表示，这样做是为了通过正弦函数和幂函数来进一步消除变换中的线性，这也是不可逆的一个原因。

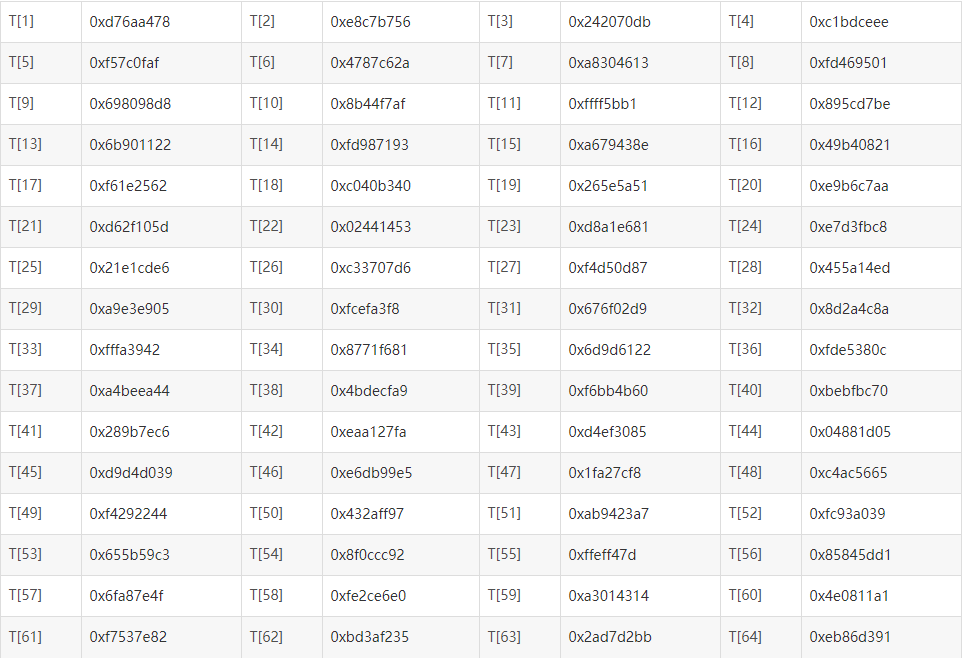
57640140382

下面利用这个常数表进行运算：

首先将我们的初始输入ABCD存起来:

1
2
3
4
5
6
7
INPUT_A = A

INPUT_B = B

INPUT_C = C

INPUT_D = D

用到的函数：F(X,Y,Z) =(X&Y)|((~X)&Z)，很明显这又是一个不可逆向的操作，下面进行运算：

循环左移：7,12,17,22，每4个为1组，一共16个数，所以进行4组

第一轮：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
A = B+((A+F(B,C,D)+M[0]+T[1])<<<7) 

D = A+((D+F(A,B,C)+M[1]+T[2])<<<12) 

C = D+((C+F(D,A,B)+M[2]+T[3])<<<17) 

B = C+((B+F(C,D,A)+M[3]+T[4])<<<22) 


A = B+((A+F(B,C,D)+M[4]+T[5])<<<7) 

D = A+((D+F(A,B,C)+M[5]+T[6])<<<12) 

C = D+((C+F(D,A,B)+M[6]+T[7])<<<17) 

B = C+((B+F(C,D,A)+M[7]+T[8])<<<22) 


A = B+((A+F(B,C,D)+M[8]+T[9])<<<7) 

D = A+((D+F(A,B,C)+M[9]+T[10])<<<12) 

C = D+((C+F(D,A,B)+M[10]+T[11])<<<17) 

B = C+((B+F(C,D,A)+M[11]+T[12])<<<22) 


A = B+((A+F(B,C,D)+M[12]+T[13])<<<7) 

D = A+((D+F(A,B,C)+M[13]+T[14])<<<12) 

C = D+((C+F(D,A,B)+M[14]+T[15])<<<17) 

B = C+((B+F(C,D,A)+M[15]+T[16])<<<22)

这里进行了移位操作和迭代操作，也是不可逆的，后面的道理是一样的。

第二轮：用到的移位是5,9,14,20，间隔为递增的4,5,6

用到的函数：G(X,Y,Z) =(X&Z)|(Y&(~Z))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
A = B+((A+G(B,C,D)+M[1]+T[17])<<<5) 

D = A+((D+G(A,B,C)+M[6]+T[18])<<<9) 

C = D+((C+G(D,A,B)+M[11]+T[19])<<<14) 

B = C+((B+G(C,D,A)+M[0]+T[20])<<<20) 

A = B+((A+G(B,C,D)+M[5]+T[21])<<<5) 

D = A+((D+G(A,B,C)+M[10]+T[22])<<<9) 

C = D+((C+G(D,A,B)+M[15]+T[23])<<<14) 

B = C+((B+G(C,D,A)+M[4]+T[24])<<<20) 

A = B+((A+G(B,C,D)+M[9]+T[25])<<<5) 

D = A+((D+G(A,B,C)+M[14]+T[26])<<<9) 

C = D+((C+G(D,A,B)+M[3]+T[27])<<<14) 

B = C+((B+G(C,D,A)+M[8]+T[28])<<<20) 

A = B+((A+G(B,C,D)+M[13]+T[29])<<<5) 

D = A+((D+G(A,B,C)+M[2]+T[30])<<<9) 

C = D+((C+G(D,A,B)+M[7]+T[31])<<<14) 

B = C+((B+G(C,D,A)+M[12]+T[32])<<<20)

第三轮：

用到的函数：H(X,Y,Z) =X^Y^Z

移位规则为7，5，7

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
A = B+((A+H(B,C,D)+M[5]+T[33])<<<4) 

D = A+((D+H(A,B,C)+M[8]+T[34])<<<11) 

C = D+((C+H(D,A,B)+M[11]+T[35])<<<16) 

B = C+((B+H(C,D,A)+M[14]+T[36])<<<23) 

A = B+((A+H(B,C,D)+M[1]+T[37])<<<4) 

D = A+((D+H(A,B,C)+M[4]+T[38])<<<11) 

C = D+((C+H(D,A,B)+M[7]+T[39])<<<16) 

B = C+((B+H(C,D,A)+M[10]+T[40])<<<23) 

A = B+((A+H(B,C,D)+M[13]+T[41])<<<4) 

D = A+((D+H(A,B,C)+M[0]+T[42])<<<11) 

C = D+((C+H(D,A,B)+M[3]+T[43])<<<16) 

B = C+((B+H(C,D,A)+M[6]+T[44])<<<23) 

A = B+((A+H(B,C,D)+M[9]+T[45])<<<4) 

D = A+((D+H(A,B,C)+M[12]+T[46])<<<11) 

C = D+((C+H(D,A,B)+M[15]+T[47])<<<16) 

B = C+((B+H(C,D,A)+M[2]+T[48])<<<23)

第四轮：移位规则为4,5,6

用到的函数：I(X,Y,Z)=Y^(X|(~Z))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
A = B+((A+I(B,C,D)+M[0]+T[49])<<<6) 

D = A+((D+I(A,B,C)+M[7]+T[50])<<<10) 

C = D+((C+I(D,A,B)+M[14]+T[51])<<<15) 

B = C+((B+I(C,D,A)+M[5]+T[52])<<<21) 

A = B+((A+I(B,C,D)+M[12]+T[53])<<<6) 

D = A+((D+I(A,B,C)+M[3]+T[54])<<<10) 

C = D+((C+I(D,A,B)+M[10]+T[55])<<<15) 

B = C+((B+I(C,D,A)+M[1]+T[56])<<<21) 

A = B+((A+I(B,C,D)+M[8]+T[57])<<<6) 

D = A+((D+I(A,B,C)+M[15]+T[58])<<<10) 

C = D+((C+I(D,A,B)+M[6]+T[59])<<<15) 

B = C+((B+I(C,D,A)+M[13]+T[60])<<<21) 

A = B+((A+I(B,C,D)+M[4]+T[61])<<<6) 

D = A+((D+I(A,B,C)+M[11]+T[62])<<<10) 

C = D+((C+I(D,A,B)+M[2]+T[63])<<<15) 

B = C+((B+I(C,D,A)+M[9]+T[64])<<<21)

至此，一个512位分组，分为M[16]，每个是32位，然后种子为A,B,C,D，常数表是T[64]，一共4大轮，每一个大轮进行了16次不同的操作，得到最新的A,B,C,D，然后我们加上之前的ABCD。

1
2
3
4
5
6
7
A = A + INPUT_A

B = B + INPUT_B

C = C + INPUT_C

D = D + INPUT_D

最终输出了A,B,C,D作为新一轮的种子序列，依次列推，最后全部输出完成，就会得到最新的ABCD作为最终的输出，也就是我们的密文，这里我个人理解，输入感觉更像是参与了加密过程，像是其中的一个key一般。

在python中已经集成了md5的算法模块，可以直接使用：

1
2
3
4
5
6
7
#coding=utf8
import hashlib
str1 = 'this is a md5 test.'
hl = hashlib.md5()
hl.update(str1.encode(encoding='utf-8'))
print('MD5加密前为 ：' + str1)
print('MD5加密后为 ：' + hl.hexdigest())

*要是想要强行碰撞的话，概率是很低的，只有1/2^64。

md5加密算法的c实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
void md5(const uint8_t *initial_msg, size_t initial_len, uint8_t *digest)
{

	// These vars will contain the hash
	uint32_t h0, h1, h2, h3;

	// Message (to prepare)
	uint8_t *msg = NULL;

	size_t new_len, offset;
	uint32_t w[16];
	uint32_t a, b, c, d, i, f, g, temp;

	// Initialize variables - simple count in nibbles:
	h0 = 0x67452301;
	h1 = 0xefcdab89;
	h2 = 0x98badcfe;
	h3 = 0x10325476;

	//Pre-processing:
	//append "1" bit to message
	//append "0" bits until message length in bits ≡ 448 (mod 512)
	//append length mod (2^64) to message

	for (new_len = initial_len + 1; new_len % (512 / 8) != 448 / 8; new_len++)
		;

	msg = (uint8_t *)malloc(new_len + 8);
	memcpy(msg, initial_msg, initial_len);
	msg[initial_len] = 0x80; // append the "1" bit; most significant bit is "first"
	for (offset = initial_len + 1; offset < new_len; offset++)
		msg[offset] = 0; // append "0" bits

	// append the len in bits at the end of the buffer.
	to_bytes(initial_len * 8, msg + new_len);
	// initial_len>>29 == initial_len*8>>32, but avoids overflow.
	to_bytes(initial_len >> 29, msg + new_len + 4);

	// Process the message in successive 512-bit chunks:
	//for each 512-bit chunk of message:
	for (offset = 0; offset < new_len; offset += (512 / 8))
	{

		// break chunk into sixteen 32-bit words w[j], 0 ≤ j ≤ 15
		for (i = 0; i < 16; i++)
			w[i] = to_int32(msg + offset + i * 4);

		// Initialize hash value for this chunk:
		a = h0;
		b = h1;
		c = h2;
		d = h3;

		// Main loop:
		for (i = 0; i < 64; i++)
		{

			if (i < 16)
			{
				f = (b & c) | ((~b) & d);
				g = i;
			}
			else if (i < 32)
			{
				f = (d & b) | ((~d) & c);
				g = (5 * i + 1) % 16;
			}
			else if (i < 48)
			{
				f = b ^ c ^ d;
				g = (3 * i + 5) % 16;
			}
			else
			{
				f = c ^ (b | (~d));
				g = (7 * i) % 16;
			}

			temp = d;
			d = c;
			c = b;
			b = b + LEFTROTATE((a + f + k[i] + w[g]), r[i]);
			a = temp;
		}

		// Add this chunk's hash to result so far:
		h0 += a;
		h1 += b;
		h2 += c;
		h3 += d;
	}

	// cleanup
	free(msg);

	//var char digest[16] := h0 append h1 append h2 append h3 //(Output is in little-endian)
	to_bytes(h0, digest);
	to_bytes(h1, digest + 4);
	to_bytes(h2, digest + 8);
	to_bytes(h3, digest + 12);
}

下面来个完整的md5算法的实现：

首先是MD5.c的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
#include <memory.h>
#include "md5.h"
 
unsigned char PADDING[]={0x80,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
                         0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
                         0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,
                         0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0};
                         
void MD5Init(MD5_CTX *context)
{
     context->count[0] = 0;
     context->count[1] = 0;
     context->state[0] = 0x67452301;
     context->state[1] = 0xEFCDAB89;
     context->state[2] = 0x98BADCFE;
     context->state[3] = 0x10325476;
}
void MD5Update(MD5_CTX *context,unsigned char *input,unsigned int inputlen)
{
    unsigned int i = 0,index = 0,partlen = 0;
    index = (context->count[0] >> 3) & 0x3F;
    partlen = 64 - index;
    context->count[0] += inputlen << 3;
    if(context->count[0] < (inputlen << 3))
       context->count[1]++;
    context->count[1] += inputlen >> 29;
    
    if(inputlen >= partlen)
    {
       memcpy(&context->buffer[index],input,partlen);
       MD5Transform(context->state,context->buffer);
       for(i = partlen;i+64 <= inputlen;i+=64)
           MD5Transform(context->state,&input[i]);
       index = 0;        
    }  
    else
    {
        i = 0;
    }
    memcpy(&context->buffer[index],&input[i],inputlen-i);
}
void MD5Final(MD5_CTX *context,unsigned char digest[16])
{
    unsigned int index = 0,padlen = 0;
    unsigned char bits[8];
    index = (context->count[0] >> 3) & 0x3F;
    padlen = (index < 56)?(56-index):(120-index);
    MD5Encode(bits,context->count,8);
    MD5Update(context,PADDING,padlen);
    MD5Update(context,bits,8);
    MD5Encode(digest,context->state,16);
}
void MD5Encode(unsigned char *output,unsigned int *input,unsigned int len)
{
    unsigned int i = 0,j = 0;
    while(j < len)
    {
         output[j] = input[i] & 0xFF;  
         output[j+1] = (input[i] >> 8) & 0xFF;
         output[j+2] = (input[i] >> 16) & 0xFF;
         output[j+3] = (input[i] >> 24) & 0xFF;
         i++;
         j+=4;
    }
}
void MD5Decode(unsigned int *output,unsigned char *input,unsigned int len)
{
     unsigned int i = 0,j = 0;
     while(j < len)
     {
           output[i] = (input[j]) |
                       (input[j+1] << 8) |
                       (input[j+2] << 16) |
                       (input[j+3] << 24);
           i++;
           j+=4; 
     }
}
void MD5Transform(unsigned int state[4],unsigned char block[64])
{
     unsigned int a = state[0];
     unsigned int b = state[1];
     unsigned int c = state[2];
     unsigned int d = state[3];
     unsigned int x[64];
     MD5Decode(x,block,64);
     FF(a, b, c, d, x[ 0], 7, 0xd76aa478); /* 1 */
 FF(d, a, b, c, x[ 1], 12, 0xe8c7b756); /* 2 */
 FF(c, d, a, b, x[ 2], 17, 0x242070db); /* 3 */
 FF(b, c, d, a, x[ 3], 22, 0xc1bdceee); /* 4 */
 FF(a, b, c, d, x[ 4], 7, 0xf57c0faf); /* 5 */
 FF(d, a, b, c, x[ 5], 12, 0x4787c62a); /* 6 */
 FF(c, d, a, b, x[ 6], 17, 0xa8304613); /* 7 */
 FF(b, c, d, a, x[ 7], 22, 0xfd469501); /* 8 */
 FF(a, b, c, d, x[ 8], 7, 0x698098d8); /* 9 */
 FF(d, a, b, c, x[ 9], 12, 0x8b44f7af); /* 10 */
 FF(c, d, a, b, x[10], 17, 0xffff5bb1); /* 11 */
 FF(b, c, d, a, x[11], 22, 0x895cd7be); /* 12 */
 FF(a, b, c, d, x[12], 7, 0x6b901122); /* 13 */
 FF(d, a, b, c, x[13], 12, 0xfd987193); /* 14 */
 FF(c, d, a, b, x[14], 17, 0xa679438e); /* 15 */
 FF(b, c, d, a, x[15], 22, 0x49b40821); /* 16 */
 
 /* Round 2 */
 GG(a, b, c, d, x[ 1], 5, 0xf61e2562); /* 17 */
 GG(d, a, b, c, x[ 6], 9, 0xc040b340); /* 18 */
 GG(c, d, a, b, x[11], 14, 0x265e5a51); /* 19 */
 GG(b, c, d, a, x[ 0], 20, 0xe9b6c7aa); /* 20 */
 GG(a, b, c, d, x[ 5], 5, 0xd62f105d); /* 21 */
 GG(d, a, b, c, x[10], 9,  0x2441453); /* 22 */
 GG(c, d, a, b, x[15], 14, 0xd8a1e681); /* 23 */
 GG(b, c, d, a, x[ 4], 20, 0xe7d3fbc8); /* 24 */
 GG(a, b, c, d, x[ 9], 5, 0x21e1cde6); /* 25 */
 GG(d, a, b, c, x[14], 9, 0xc33707d6); /* 26 */
 GG(c, d, a, b, x[ 3], 14, 0xf4d50d87); /* 27 */
 GG(b, c, d, a, x[ 8], 20, 0x455a14ed); /* 28 */
 GG(a, b, c, d, x[13], 5, 0xa9e3e905); /* 29 */
 GG(d, a, b, c, x[ 2], 9, 0xfcefa3f8); /* 30 */
 GG(c, d, a, b, x[ 7], 14, 0x676f02d9); /* 31 */
 GG(b, c, d, a, x[12], 20, 0x8d2a4c8a); /* 32 */
 
 /* Round 3 */
 HH(a, b, c, d, x[ 5], 4, 0xfffa3942); /* 33 */
 HH(d, a, b, c, x[ 8], 11, 0x8771f681); /* 34 */
 HH(c, d, a, b, x[11], 16, 0x6d9d6122); /* 35 */
 HH(b, c, d, a, x[14], 23, 0xfde5380c); /* 36 */
 HH(a, b, c, d, x[ 1], 4, 0xa4beea44); /* 37 */
 HH(d, a, b, c, x[ 4], 11, 0x4bdecfa9); /* 38 */
 HH(c, d, a, b, x[ 7], 16, 0xf6bb4b60); /* 39 */
 HH(b, c, d, a, x[10], 23, 0xbebfbc70); /* 40 */
 HH(a, b, c, d, x[13], 4, 0x289b7ec6); /* 41 */
 HH(d, a, b, c, x[ 0], 11, 0xeaa127fa); /* 42 */
 HH(c, d, a, b, x[ 3], 16, 0xd4ef3085); /* 43 */
 HH(b, c, d, a, x[ 6], 23,  0x4881d05); /* 44 */
 HH(a, b, c, d, x[ 9], 4, 0xd9d4d039); /* 45 */
 HH(d, a, b, c, x[12], 11, 0xe6db99e5); /* 46 */
 HH(c, d, a, b, x[15], 16, 0x1fa27cf8); /* 47 */
 HH(b, c, d, a, x[ 2], 23, 0xc4ac5665); /* 48 */
 
 /* Round 4 */
 II(a, b, c, d, x[ 0], 6, 0xf4292244); /* 49 */
 II(d, a, b, c, x[ 7], 10, 0x432aff97); /* 50 */
 II(c, d, a, b, x[14], 15, 0xab9423a7); /* 51 */
 II(b, c, d, a, x[ 5], 21, 0xfc93a039); /* 52 */
 II(a, b, c, d, x[12], 6, 0x655b59c3); /* 53 */
 II(d, a, b, c, x[ 3], 10, 0x8f0ccc92); /* 54 */
 II(c, d, a, b, x[10], 15, 0xffeff47d); /* 55 */
 II(b, c, d, a, x[ 1], 21, 0x85845dd1); /* 56 */
 II(a, b, c, d, x[ 8], 6, 0x6fa87e4f); /* 57 */
 II(d, a, b, c, x[15], 10, 0xfe2ce6e0); /* 58 */
 II(c, d, a, b, x[ 6], 15, 0xa3014314); /* 59 */
 II(b, c, d, a, x[13], 21, 0x4e0811a1); /* 60 */
 II(a, b, c, d, x[ 4], 6, 0xf7537e82); /* 61 */
 II(d, a, b, c, x[11], 10, 0xbd3af235); /* 62 */
 II(c, d, a, b, x[ 2], 15, 0x2ad7d2bb); /* 63 */
 II(b, c, d, a, x[ 9], 21, 0xeb86d391); /* 64 */
     state[0] += a;
     state[1] += b;
     state[2] += c;
     state[3] += d;
}

然后是MD5.h

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#ifndef MD5_H
#define MD5_H
 
typedef struct
{
    unsigned int count[2];
    unsigned int state[4];
    unsigned char buffer[64];   
}MD5_CTX;
 
                         
#define F(x,y,z) ((x & y) | (~x & z))
#define G(x,y,z) ((x & z) | (y & ~z))
#define H(x,y,z) (x^y^z)
#define I(x,y,z) (y ^ (x | ~z))
#define ROTATE_LEFT(x,n) ((x << n) | (x >> (32-n)))
#define FF(a,b,c,d,x,s,ac) \
          { \
          a += F(b,c,d) + x + ac; \
          a = ROTATE_LEFT(a,s); \
          a += b; \
          }
#define GG(a,b,c,d,x,s,ac) \
          { \
          a += G(b,c,d) + x + ac; \
          a = ROTATE_LEFT(a,s); \
          a += b; \
          }
#define HH(a,b,c,d,x,s,ac) \
          { \
          a += H(b,c,d) + x + ac; \
          a = ROTATE_LEFT(a,s); \
          a += b; \
          }
#define II(a,b,c,d,x,s,ac) \
          { \
          a += I(b,c,d) + x + ac; \
          a = ROTATE_LEFT(a,s); \
          a += b; \
          }                                            
void MD5Init(MD5_CTX *context);
void MD5Update(MD5_CTX *context,unsigned char *input,unsigned int inputlen);
void MD5Final(MD5_CTX *context,unsigned char digest[16]);
void MD5Transform(unsigned int state[4],unsigned char block[64]);
void MD5Encode(unsigned char *output,unsigned int *input,unsigned int len);
void MD5Decode(unsigned int *output,unsigned char *input,unsigned int len);
 
#endif

最后是使用方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include "md5.h"
#include "base64.h"
//	123456 
// 	{enc8}asL1gFOqmbh5FtMe6KP3UHBJfGA=
// 　{enc8}fZHJJ24JsRNCAHtX5l0yoFhJfGA=
int main(int argc, char *argv[])
{
	unsigned char enc[] = "EUxNIpbzGlnJbM4KKjYl+za4fmA=";
	int i;
	unsigned char encrypt[] ="123456";
	unsigned char *buf =NULL;
	unsigned char decrypt[24];
	int dest[0x80];
	MD5_CTX md5;
	int time_from = 1618917420;//2021-4-20-19-17
	int time_to = 1618917600;//2021-4-20-19-20
	for(int time = time_from;time<=time_to;time++)
	{
		memset(decrypt,0,24);
		memset(dest,0,0x80);  
		MD5Init(&md5);       
		MD5Update(&md5,encrypt,strlen((char *)encrypt));  		
		MD5Update(&md5,&time,4);
		MD5Final(&md5,decrypt);        
		memcpy(&dest, &decrypt, 0x10);
		dest[4] = time;
		buf = base64_encode(dest);
		if(!strcmp(enc,buf))
		{
			printf("Congratulation!\n");
			printf("Time--->%d\n",time);
			break;
		}
		free(buf);
		*buf = NULL;
	}
	return 0;
}

主要就是Init再Update最后再Final就可以实现加密了，上面是个简单的例子。

二、Hash函数研究

hash函数又称为散列函数，其主要目的是将不定长度的消息转成固定长度的消息，一般存在着一种映射关系，有个映射表，一般有2个特点需要记住的是：

1、抗碰撞能力：

对于任意两个不同的数据块，其hash值相同的可能性极小；对于一个给定的数据块，找到和它hash值相同的数据块极为困难。

但是并不是说没有，可以举个MD5的例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import hashlib

#  两段HEX字节串，注意它们有细微差别
a = bytearray.fromhex("0e306561559aa787d00bc6f70bbdfe3404cf03659e704f8534c00ffb659c4c8740cc942feb2da115a3f4155cbb8607497386656d7d1f34a42059d78f5a8dd1ef")

b = bytearray.fromhex("0e306561559aa787d00bc6f70bbdfe3404cf03659e744f8534c00ffb659c4c8740cc942feb2da115a3f415dcbb8607497386656d7d1f34a42059d78f5a8dd1ef")

#  输出MD5，它们的结果一致
print(hashlib.md5(a).hexdigest())
print(hashlib.md5(b).hexdigest())

### a和b输出结果都为：
cee9a457e790cf20d4bdaa6d69f01e41
cee9a457e790cf20d4bdaa6d69f01e41
2、抗篡改能力：

对于一个数据块，哪怕只改动其一个比特位，其hash值的改动也会很大

1
2
MD5("version1") = "966634ebf2fc135707d6753692bf4b1e";
MD5("version2") = "2e0e95285f08a07dea17e7ee111b21c8";

经常使用的构造散列函数的方法
散列函数能使对一个数据序列的訪问过程更加迅速有效，通过散列函数，数据元素将被更快地定位：

  1. 直接寻址法：取keyword或keyword的某个线性函数值为散列地址。即H(key)=key或H(key) = a•key + b，当中a和b为常数（这样的散列函数叫做自身函数）

  2. 数字分析法：分析一组数据，比方一组员工的出生年月日，这时我们发现出生年月日的前几位数字大体同样，这种话，出现冲突的几率就会非常大，可是我们发现年月日的后几位表示月份和详细日期的数字区别非常大，假设用后面的数字来构成散列地址，则冲突的几率会明显减少。因此数字分析法就是找出数字的规律，尽可能利用这些数据来构造冲突几率较低的散列地址。

  3. 平方取中法：取keyword平方后的中间几位作为散列地址。

  4. 折叠法：将keyword切割成位数同样的几部分，最后一部分位数能够不同，然后取这几部分的叠加和（去除进位）作为散列地址。

  5. 随机数法：选择一随机函数，取keyword的随机值作为散列地址，通经常使用于keyword长度不同的场合。

  6. 除留余数法：取keyword被某个不大于散列表表长m的数p除后所得的余数为散列地址。即 H(key) = key MOD p, p<=m。不仅能够对keyword直接取模，也可在折叠、平方取中等运算之后取模。对p的选择非常重要，一般取素数或m，若p选的不好，容易产生同义词。

目前流行的 Hash 算法包括 MD5、SHA-1 和 SHA-2。

  • MD4（RFC 1320）是 MIT 的 Ronald L. Rivest 在 1990 年设计的，MD 是 Message Digest 的缩写。其输出为 128 位。MD4 已证明不够安全。
  • MD5（RFC 1321）是 Rivest 于1991年对 MD4 的改进版本。它对输入仍以 512 位分组，其输出是 128 位。MD5 比 MD4 复杂，并且计算速度要慢一点，更安全一些。MD5 已被证明不具备”强抗碰撞性”。
  • SHA （Secure Hash Algorithm）是一个 Hash 函数族，由 NIST（National Institute of Standards and Technology）于 1993 年发布第一个算法。目前知名的 SHA-1 在 1995 年面世，它的输出为长度 160 位的 hash 值，因此抗穷举性更好。SHA-1 设计时基于和 MD4 相同原理，并且模仿了该算法。SHA-1 已被证明不具”强抗碰撞性”。
  • 为了提高安全性，NIST 还设计出了 SHA-224、SHA-256、SHA-384，和 SHA-512 算法（统称为 SHA-2），跟 SHA-1 算法原理类似。SHA-3 相关算法也已被提出。

3、sha256的c语言实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
#include<stdio.h>
#include<windows.h>
typedef unsigned int u32;
typedef unsigned char u8;
typedef unsigned long long u64;
#define H0  0x6a09e667
#define H1  0xbb67ae85
#define H2  0x3c6ef372
#define H3  0xa54ff53a
#define H4  0x510e527f
#define H5  0x9b05688c
#define H6  0x1f83d9ab
#define H7  0x5be0cd19
u32 Wt[64];
u32 Kt[64] = { 0x428a2f98, 0x71374491, 0xb5c0fbcf, 0xe9b5dba5,
				0x3956c25b, 0x59f111f1, 0x923f82a4, 0xab1c5ed5,
				0xd807aa98, 0x12835b01, 0x243185be, 0x550c7dc3,
				0x72be5d74, 0x80deb1fe, 0x9bdc06a7, 0xc19bf174,
				0xe49b69c1, 0xefbe4786, 0x0fc19dc6, 0x240ca1cc,
				0x2de92c6f, 0x4a7484aa, 0x5cb0a9dc, 0x76f988da,
				0x983e5152, 0xa831c66d, 0xb00327c8, 0xbf597fc7,
				0xc6e00bf3, 0xd5a79147, 0x06ca6351, 0x14292967,
				0x27b70a85, 0x2e1b2138, 0x4d2c6dfc, 0x53380d13,
				0x650a7354, 0x766a0abb, 0x81c2c92e, 0x92722c85,
				0xa2bfe8a1, 0xa81a664b, 0xc24b8b70, 0xc76c51a3,
				0xd192e819, 0xd6990624, 0xf40e3585, 0x106aa070,
				0x19a4c116, 0x1e376c08, 0x2748774c, 0x34b0bcb5,
				0x391c0cb3, 0x4ed8aa4a, 0x5b9cca4f, 0x682e6ff3,
				0x748f82ee, 0x78a5636f, 0x84c87814, 0x8cc70208,
				0x90befffa, 0xa4506ceb, 0xbef9a3f7, 0xc67178f2 };
u32 Ch(u32 x, u32 y, u32 z)
{
	return (x & y) ^ (~x & z);
}
u32 cycle_rshift(u32 x,u32 n)
{
	return 	((x & (((u32)1 << n) - 1)) << (32 - n))|(x >> n);
}
u32 Sum0(u32 x)
{
	return cycle_rshift(x, 2) ^ cycle_rshift(x, 13) ^ cycle_rshift(x, 22);
}
u32 Sum1(u32 x)
{
	return cycle_rshift(x, 6) ^ cycle_rshift(x, 11) ^ cycle_rshift(x, 25);
}
u32 Sigma0(u32 x)
{
	return cycle_rshift(x, 7) ^ cycle_rshift(x, 18) ^ (x>>3);
}
u32 Sigma1(u32 x)
{
	return cycle_rshift(x, 17) ^ cycle_rshift(x, 19) ^ (x >> 10);
}
u32 Ma(u32 x, u32 y, u32 z)
{
	return (x & y) ^ (x & z)^ (y & z);
}
struct sha256
{
	u32 block[16];	//加密的measage
	u32 hash[8];	//hash的结果
	u64 hash_length;//总共hash的byte数
	u8  offset;		//一个update未对齐Word(4字节)的字节数
	u8  index;		//当前已经写到block的位置
};
void sha_init(struct sha256 *s)
{
	s->hash[0] = H0;
	s->hash[1] = H1;
	s->hash[2] = H2;
	s->hash[3] = H3;
	s->hash[4] = H4;
	s->hash[5] = H5;
	s->hash[6] = H6;
	s->hash[7] = H7;
	s->hash_length = 0;
	s->index  = 0;
	s->offset = 0;
}
void sha_caculator(struct sha256* s)//先补齐 Wt,然后循环64次加密
{
	u8 i = 0;
	u32 m0, s0, s1,c1,t1;

	u32 temp[8];
	for(i=0;i<8;i++)
		temp[i]=s->hash[i];

	for (i = 0; i < 16; i++)
		Wt[i] = s->block[i];

	for (i = 16; i < 64; i++)
		Wt[i] = Sigma1(Wt[i-2])+ Wt[i-7]+Sigma0(Wt[i - 15])+ Wt[i - 16];
	
	for (i = 0; i < 64; i++)
	{
		s0 = Sum0(temp[0]);

		s1 = Sum1(temp[4]);

		m0 = Ma(temp[0], temp[1], temp[2]);

		c1 = Ch(temp[4], temp[5], temp[6]);

		t1 = s1+c1+temp[7]+Wt[i] + Kt[i];

		temp[7] = temp[6];
		temp[6] = temp[5];
		temp[5] = temp[4];
		temp[4] = temp[3]+ t1;
		temp[3] = temp[2];
		temp[2] = temp[1];
		temp[1] = temp[0];
		temp[0] = t1+m0+s0;
	
	}

	for (i = 0; i < 8; i++)
		s->hash[i]+=temp[i];
}
void sha_updata(struct sha256* s,unsigned char *str,u64 len)
{
	u64 i = 0;
	u64 count;
	s->hash_length += len;
	if (s->offset!=0)//说明没有4字节对齐
	{
		if (s->offset + len < 4)
		{
			for (i = s->offset; i < s->offset+len; i++)
			{
				s->block[s->index]  |= (((u32)(*str)) << (8 * (3 - i)));
				str++;
			}
			s->offset += len;
			return;
		}
		else
		{
			len = len + s->offset - 4;
			for (i = s->offset; i < 4; i++)
			{
				s->block[s->index]  |= (((u32)(*str)) << (8 * (3 - i)));
				str++;
			}
			s->index++;
			if (s->index == 16)
			{
				sha_caculator(s);//满足512bit 16Word加密一次
				s->index = 0;
			}
		}
	}
	count = (len >> 2);//计算这次加密有多少个Word
	s->offset = len % 4;//对齐Word剩余的byte


	for(i=0;i<count;i++)
	{

		s->block[s->index] = (((u32)(*str))		<< 24) |
								((*(str	+	1))		<< 16) |
								((*(str + 2))	<< 8) |
								(*(str + 3));
		s->index++;

		str += 4;

		if (s->index == 16)
		{
			sha_caculator(s);//满足512bit 16Word加密一次
			s->index = 0;
		}
	}


	s->block[s->index] = 0;//对齐Word剩余的byte写在 s->index 位置上，供下一次update使用

	for (i = 0; i < s->offset; i++)
	{
		s->block[s->index] |= (((u32)(*str)) << (8 * (3 - i)));
		str++;
	}
	
}
void sha_final(struct sha256* s)
{
	u8 temp=s->hash_length % 64;//计算需要填充多少byte
	u8 fill[4] = { 0x80,0x0,0x0,0x0 };
	u32 i;
	if (temp == 56)//则需要填充一个512bit
	{
		//补齐前一次的512bit
		if (s->offset != 0)
		{
			for (i = 0; i < 4-s->offset; i++)
			s->block[s->index]  |= (fill[i]<< (8 * (3 - i-s->offset)));

			s->index++;
		}
		else
		{
			s->block[s->index] = 0x80000000;
			s->index++;
		}
		for (i = s->index; i < 16; i++)
			s->block[i] = 0;

		sha_caculator(s);

	
		for(i=0;i<14;i++)
		s->block[i] = 0;

		s->block[14] = s->hash_length >> 29;
		s->block[15] = s->hash_length << 3 & 0xffffffff;
		sha_caculator(s);

	}
	else
	{
		if (s->offset != 0)
		{
			for (i = 0; i < 4-s->offset; i++)
				s->block[s->index]  |= (fill[i] << (8 * ( 3 - i - s->offset)));

			s->index++;
		}
		else
		{
			s->block[s->index] = 0x80000000;
			s->index++;
		}
		for (i = s->index; i < 14; i++)
			s->block[i] = 0;
		s->block[14] = s->hash_length>> 29;
		s->block[15] = s->hash_length<<3 & 0xffffffff;
		sha_caculator(s);
	}
}
int main()
{
	

	int i = 0;
	struct sha256 testsha;

	sha_init(&testsha);
	sha_updata(&testsha, "abc", 3);
	sha_updata(&testsha, "defg", 4);
	sha_updata(&testsha, "hi", 2);
	sha_updata(&testsha, "jklmn", 5);
	sha_final(&testsha);

	for (i = 0; i < 8; i++)
		printf("%08x", testsha.hash[i]);

	system("pause");




}

以后看table行事，猜测出加密的算法。

V1ct0r

Where there is a will,there is a way！
0%